Estadística clásica

Las técnicas estadísticas clásicas (descriptivas, correlacionales e inferenciales) se han empleado de manera generalizada en el ámbito educativo para extraer información valiosa a partir de bases de datos. Estas técnicas nos sirven para organizar y resumir la información, de cara a facilitar extraer conclusiones útiles para el entorno educativo. No obstante, las bases de datos manejadas solían ser de un tamaño manejable, tanto en número de sujetos como en número de variables.
Con la llegada de la Sociedad Digital, se comienza a trabajar con una mayor cantidad de información. Se generalizan entonces las evaluaciones a gran escala, que disponen de volúmenes de información excesivos para las técnicas anteriores. La estadística clásica es menos eficaz para detectar patrones cuando los datos son masivos, resultando poco flexible e informativa.

   Minería de datos: Árboles de decisión

La minería de datos (Data mining) contempla un conjunto de técnicas diseñadas específicamente para detectar patrones en volúmenes masivos de datos. Y los árboles de decisión, una de las técnicas más extendidas de la minería de datos, tratan de predecir o explicar en qué puntuación se situarán los sujetos de una muestra en una variable (llamada variable criterio), a partir del conocimiento de las puntuaciones obtenidas en un conjunto de variables explicativas o predictoras.

Así, losárboles de decisión pueden resultar valiosos en el estudio de la eficacia escolar cuando disponemos de bases de datos con miles de sujetos y cientos de variables explicativas (como ocurre en la evaluación PISA). En la práctica, se selecciona como variable criterio la pertenencia del profesor, equipo directivo o estudiante a una escuela de alta o baja eficacia, y como variables predictoras todo el resto de factores de proceso susceptibles de ser asociados a la eficacia. Así, el árbol selecciona las variables que diferencian mejor entre los sujetos de alta y baja eficacia, es decir, los factores asociados a la eficacia. Analicemos el ejemplo siguiente, en el que se muestra un árbol de decisión ficticio para una muestra de estudiantes.

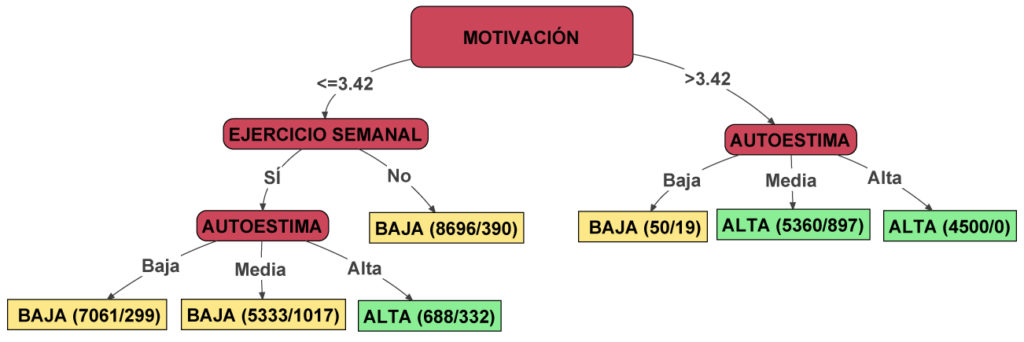
El árbol muestra varios caminos hasta llegar a las hojas finales (rectángulos). Así, todas las elipses granates (o cortes) equivalen a variables explicativas, las líneas que las siguen (o ramas) indican las posibles puntuaciones de los sujetos en la variable anterior y cada hoja muestra en qué tipo de escuela es más probable que esté el estudiante que pertenece a ese grupo. En estas hojas aparecen 2 números, el primero referido al total de estudiantes que obtuvo las puntuaciones señaladas en las variables explicativas y el segundo al número de estudiantes que no pertenecen al tipo de escuela señalado (de entre todos los anteriores).

Así, en el ejemplo hay 50 estudiantes de autoestima baja con un nivel de motivación superior a 3.42 puntos. De hecho, si un sujeto obtiene estas puntuaciones, es más probable que pertenezca a una escuela de baja eficacia. No obstante, 19 de esos 50 estudiantes no pertenecen realmente a escuelas de baja eficacia, lo que supone un 38% del total (19/50*100). Por lo tanto, esta predicción tiene una precisión del 62%.

Por otro lado, los 4500 estudiantes de motivación superior a 3.42 y autoestima alta pertenecen a centros de alta eficacia, por lo que esta predicción tiene un 100% de precisión. Esto supone que, en la población, los estudiantes con motivaciones y autoestimas altas se asocian claramente a la alta eficacia. Por otro lado, parece que las motivaciones más bajas se asocian más claramente a la baja eficacia, incluso en el caso de estudiantes de autoestimas medias que realizan ejercicio semanal.

Viendo este árbol, podríamos concluir, por tanto, lo siguiente:

• La variable motivación está claramente asociada a la eficacia escolar. Niveles de motivación altos se asocian a la eficacia escolar.
• Ante niveles de motivación alta, la autoestima baja es un factor de riesgo de la eficacia escolar.
• Ante niveles de motivación baja, el ejercicio semanal y la autoestima pueden proteger la eficacia escolar, aunque el nivel de asociación es leve en este caso.